Hello everyone!
I actually have some good news: CuSolver xgeev is working in my torch and I am just preparing the PR now. There are some problems with testing. I will discuss them in a dedicated topic on this forum.
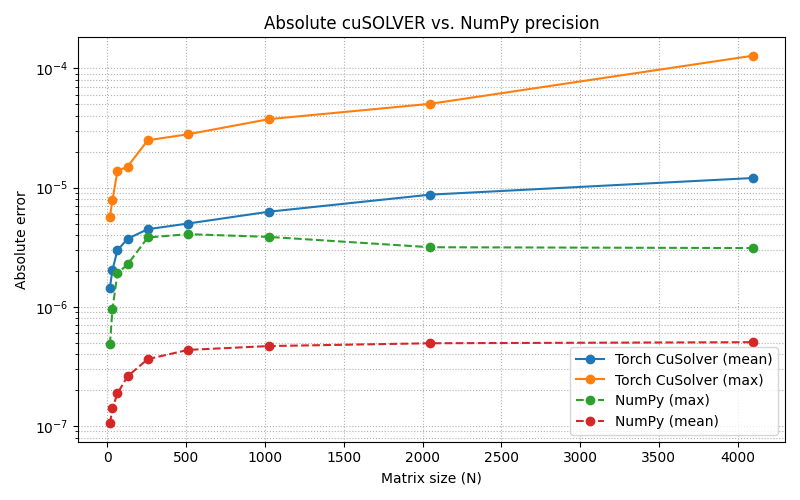
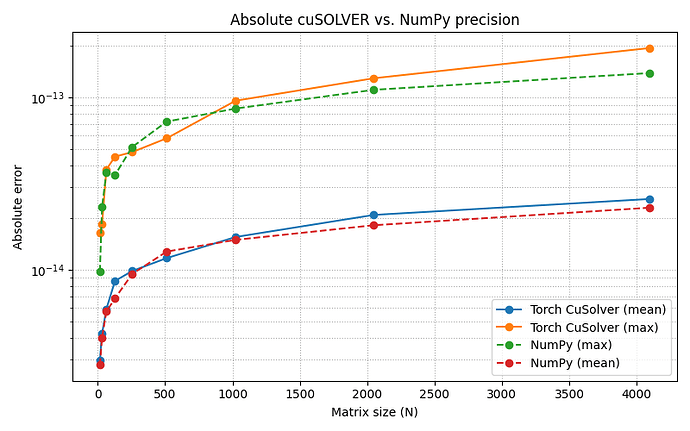
In the meantime, I did some testing regarding the precision of the xgeev algorithm using the eigenvalue equation. So the eigenvalues are defined by saying l * v - A * v = 0. What I did now is evaluate how large the left-hand side of that equation is for the tried and tested NumPy eig implementation and my new algorithm. What I found is that the double precision versions are pretty close (float64 and complex128), but the single precision version of the algorithm seems to be about one to two orders of magnitude worse than NumPy for the matrix sizes I tested.
I hope this will provide some room for discussions in regards to my pull request and also possibly for evaluating torch’s future behavior when choosing backends.
Kind regards, and as always, happy to receive any input.